Stochastic optimization of the simulated life-cycle of ill cows to provide an advice for farmers when to sell
 Kutatás vezetője: Bánhelyi Balázs
Kutatás vezetője: Bánhelyi Balázs
Intézmény: University of Szeged
Leírás:A partner tejüzem történelmi adatai alapján a feladatunk egy olyan modell meghatározása, amellyel modellezhetjük azt a gazdasági döntési, hogy a megbetegedett tehenet meggyógyítsák és tovább tartását vagy eladják. A rendelkezésre álló adatokból szeretnénk a legjövedelmezőbb döntést meghozni. Más szempontból azt a célt tűzzük ki célul, hogy a gazdálkodók optimalizálhassák a gazdaság teheneinek összetételét a jobb jövedelmezőség érdekében.
Given all the historic data of the dairy farm, our task is to determine how to model the economic decision problem in such a way that the user will become capable to decide on the keeping or selling of the given cow that became ill in such a way that according to the available data the most profitable decision could be met. In a different viewpoint, we aim to have a system that enables the farmers to optimize the composition of the farm’s cows for better profitability.
One of the most unpredictable, the most profit sensitive sector of the common section of agriculture and economy is milk production. Since the anticipated milk price is volatile, we have to design scalable models to get efficient solutions. We investigate the possibility of effective economic modelling of an important decision: when to sell the cow after a diagnosed new mastitis illness. After visiting a few local farms, and getting to know more about the problem, we can say, that usually they sell a cow when it is in a very bad shape.
So far it looks like a cow is treated with the proper medicine once it gets ill with mastitis, and it is kept – if it is not in a really bad shape that it has to be sold. Using some mathematics, simulations and programming we can estimate the expected profit of an animal if we keep it or sell it. This way farmers do not have to keep unprofitable cows.
A project like this requires close cooperation between programmers and agriculture workers. Using the most important factors of a cow’s life we have built a pretty simple but hopefully detailed enough model.
With just a few information we can simulate the future of a cow. The starting data includes some data about the cow from the age to the illness number. And we also calculated some probabilities to make our decisions more realistic from some historical data. For example with the higher number of mastitis it will be more likely that a cow gets ill again. Although the milk production of a cow follows a specific curve, the dairy cycle curve, according to our computational tests, to optimize the purchasing decision, we can assume that the milk production is constant within the dairy cycle.
All of the profits in different states of the cow can be calculated from the data which is collected in dairy farms, or using dispersion, or even using the daily data from local dairy farms’ databases.
With our microsimulation model we investigate the possible best way to decide when to sell the ill cow. The basis of our technique is to simulate the life of a cow on daily basis. In other words, we start with a cow of a given age, number of already suffered mastitis illness, and in a given phase of the dairy cycle. For each day we check a list of possible events in the life of a cow. If an event is possible then we generate a random number to simulate a realistic experiment. This way we generate a list of events for the rest of the cow’s life. So we can manage multiple events at the same time. For example we can keep on counting the lactation cycle days, while the cow is ill. While computing the possible events we use the same which were used during the calculation of our data. So the methods to determine the possible events can rely on fixed data, probability dispersion, or even a full list of historical data.
A few regularities can be discovered, like after a proper dry period, the milk production will resume. The cycle of that cow ends by its selling. The date of the purchase can be determined by our simple rule of thumb: we sell the cow if it reaches either the 6th mastitis, or its 10th year of living.
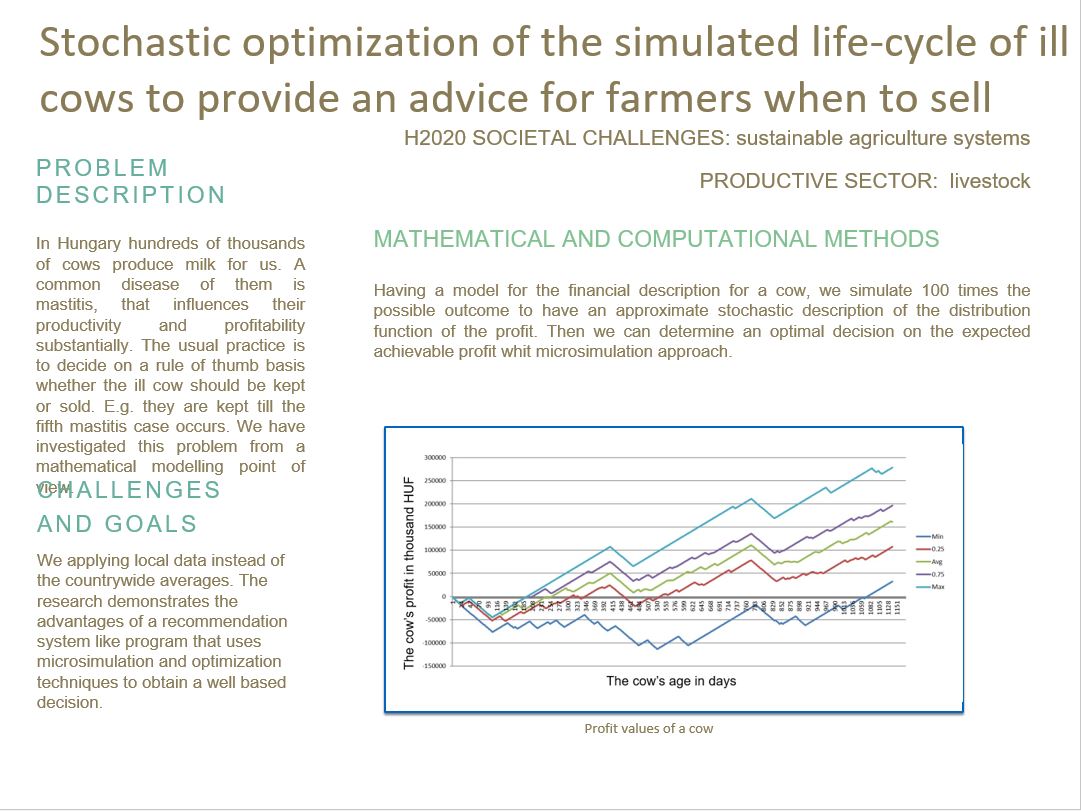
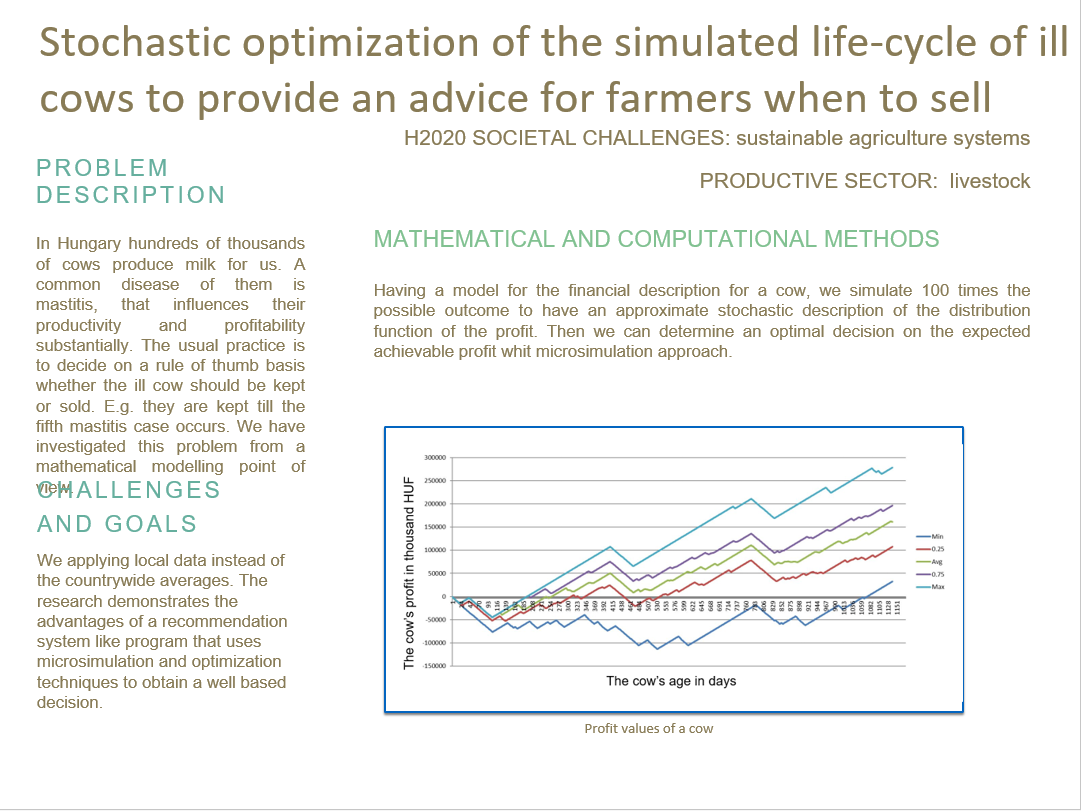
Having a model for the financial description for a cow, we simulate 100 times the possible outcome to have an approximate stochastic description of the distribution function of the profit. Then we can determine an optimal decision on the expected achievable profit.